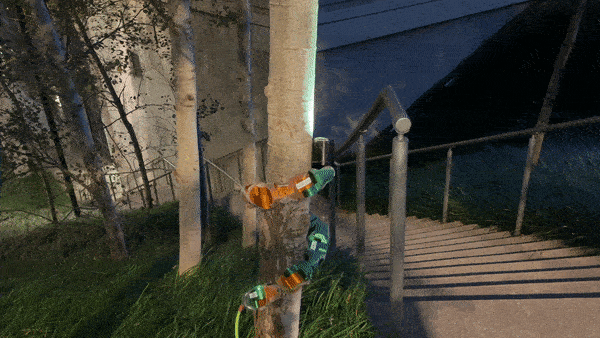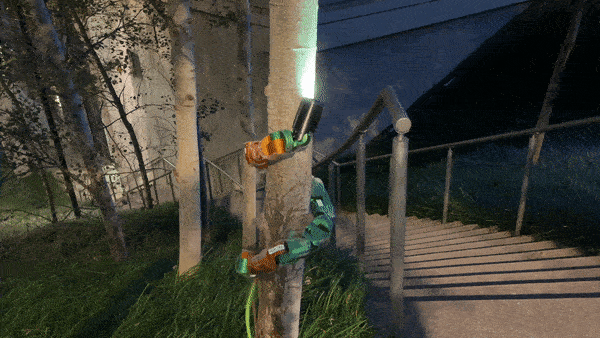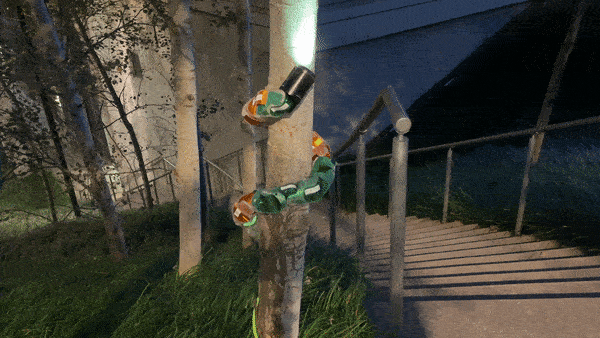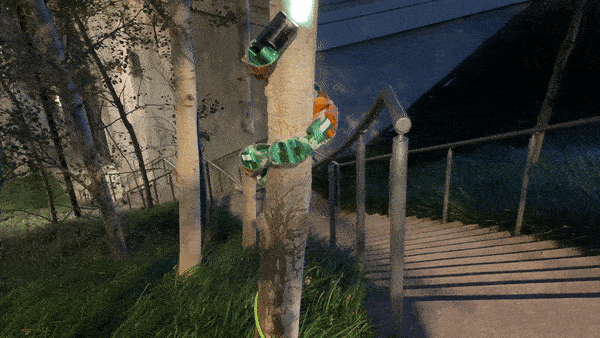ReU snake robot performing pole climbing
Abstract
SnakeLib is a ROS-based package that holds past gait research on modular snake robots and serves as a platform to facilitate further development. SnakeLib’s basic gait implementations provide a user-friendly and intuitive way to operate the robot with a joystick.
Contributions
- A set of ROS packages for simulating and controlling Biorobotics Lab snake robots.
- ROS based software to control ReU, SEA, and RSnake snake robots, receive sensor feedback, and create visualizations.
- ROS diagram
- HEBI ros node for sending joint commands to HEBI electronics and reading sensor feedback
- Camera node to read camera in the ReU snakehead
- Gait library to host manually programmed snake gaits
- Joystick node to convert joystick inputs to snake commands
- Robot class for easy to use IK and FK implementations
- RViz and PyQt based GUI to visualize state and camera feedback
- Snake state node for virtual chassis implementation for robot state visualization
- GUI node to create PyQt interface
Demos
Sidewinding
Summary
$$ \alpha(n, t) = \beta_{even} + A_{even}sin(\omega_{t, even}t + \omega_{s, even}n) \forall \text{even n} $$ $$ \alpha(n, t) = \beta_{odd} + A_{odd}sin(\omega_{t, odd} + \omega_{s, odd}n) \forall \text{odd n} $$ Sideways moving gait inspired by snake's sidewinding motion.Rolling
Summary
$$ \alpha(n, t) = \beta_{even} + A_{even}sin(\omega_{t, even}t + \omega_{s, even}n) \forall \text{even n} $$ $$ \alpha(n, t) = \beta_{odd} + A_{odd}sin(\omega_{t, odd} + \omega_{s, odd}n) \forall \text{odd n} $$ Sideways moving gait inspired rolling motion of a body. Here, the wave only propogates in time (i.e., $\omega_s = 0$) and the horizontal and vertical waves are offset by $\pi/2$.Linear progression
Summary
$$ \alpha(n, t) = \beta_{even} + A_{even}sin(\omega_{t, even}t + \omega_{s, even}n) \forall \text{even n} $$ $$ \alpha(n, t) = \beta_{odd} + A_{odd}sin(\omega_{t, odd} + \omega_{s, odd}n) \forall \text{odd n} $$Pole climbing
Summary
IK-based headlook
Summary
$$ \dot{q} = J(q)^{+}v $$ Here,$\dot{q}$: Joint velocities
$J^{+}$: Pseudo-inverse of the jacobian
$v$: End-effector velocity
Controls the end-effector (snake head) in cartesian space using inverse jacobian approach.
Slithering
Summary
Forward moving gait inspired by snake's [slithering](https://en.wikipedia.org/wiki/Snake_locomotion#Slithering) motion.Turn-in-place
Summary
$$ \alpha(n, t) = \beta_{even} + A_{even}sin(\omega_{t, even}t + \omega_{s, even}n) \forall \text{even n} $$ $$ \alpha(n, t) = \beta_{odd} + A_{odd}sin(\omega_{t, odd} + \omega_{s, odd}n) \forall \text{odd n} $$ Implemented by running opposite direction sidewinding gait in two halfs of the snake robot.